CCA 1 and CCA 2

CCA 1 and CCA 2

CCA 安全是有两个的，即是 IND-CCA 1 和 IND-CCA 2，这两种 CCA 是有区别的。

CCA 安全

CCA的全称是Chosen-ciphertext attack，也就是选择密文攻击，对比CPA安全，CCA中的攻击者可以访问解密机，而选择明文CPA中吗，攻击者只有加密机的访问权限。我们需要用数学语言来描述CCA。

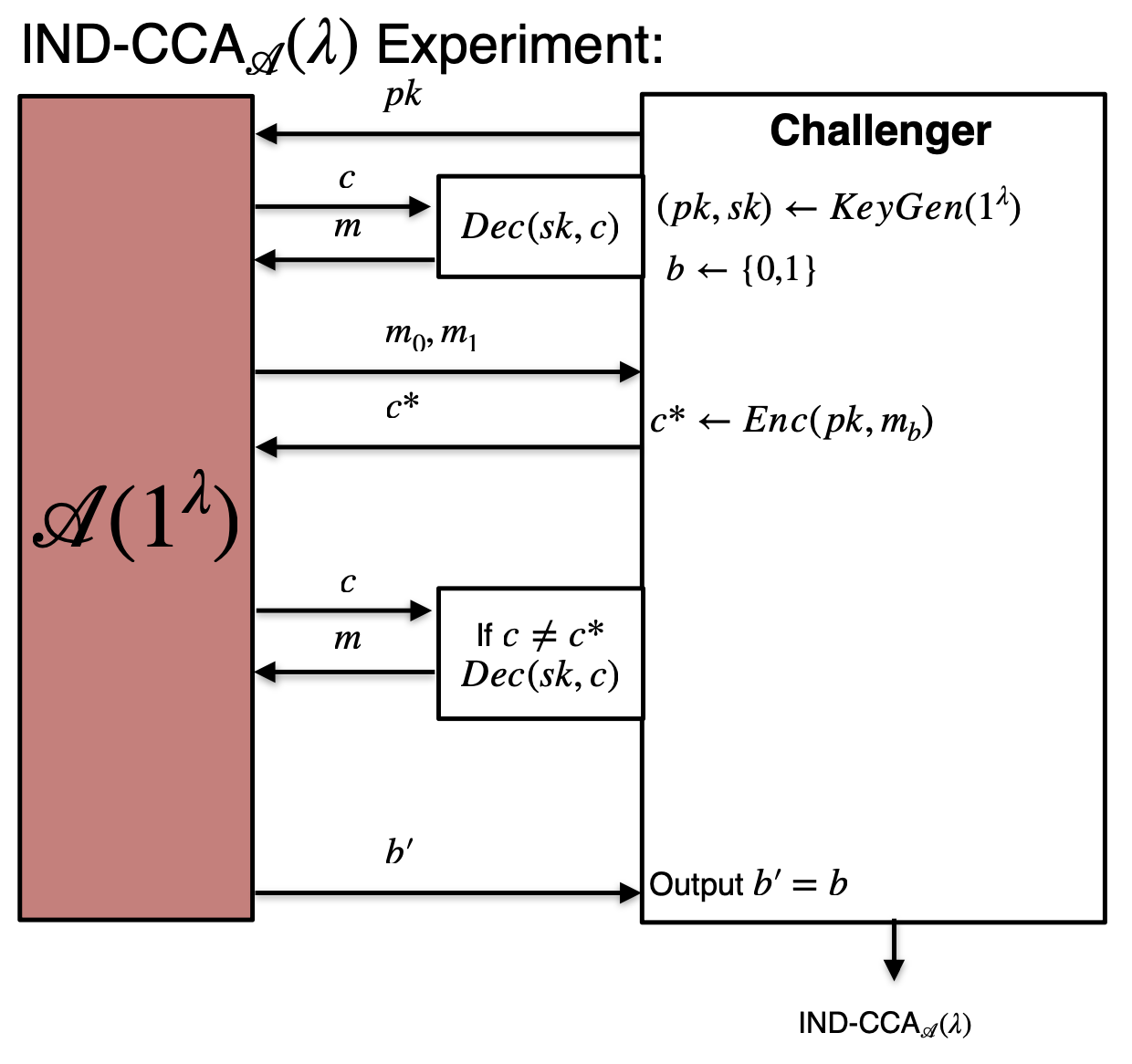
CCA 实验

1. 加密方案生成一个公私钥对$(pk,sk)$ ，其中 $pk$ 是公钥，$sk$ 是私钥。公钥公开给攻击者。
2. 攻击者可以选择多个密文并提交给解密算法，Challenger 会返回每个密文的解密结果给攻击者。攻击者可以重复这一过程。
3. 挑战阶段:
   • 攻击者提交两个等长的明文 $m_0$ 和 $m_1$ 给Challenger。
   • Challenger 随机挑选一个$b \in {0, 1}$，并加密明文 $m_b$ 得到密文 $c^*$ ，返回给攻击者。
4. * 攻击者可以继续选择密文得到这些密文的解密结果，但是不能查询$c^*$的解密结果（非常显然）。
5. 攻击者通过分析，猜测 $b$ 的值，即判断返回的密文是 $m_0$ 还是 $m_1$ 的加密结果。
6. 如果攻击者猜测成功的概率显著高于随机猜测（即 $\frac{1}{2}$），则认为加密方案在 CCA 不安全。

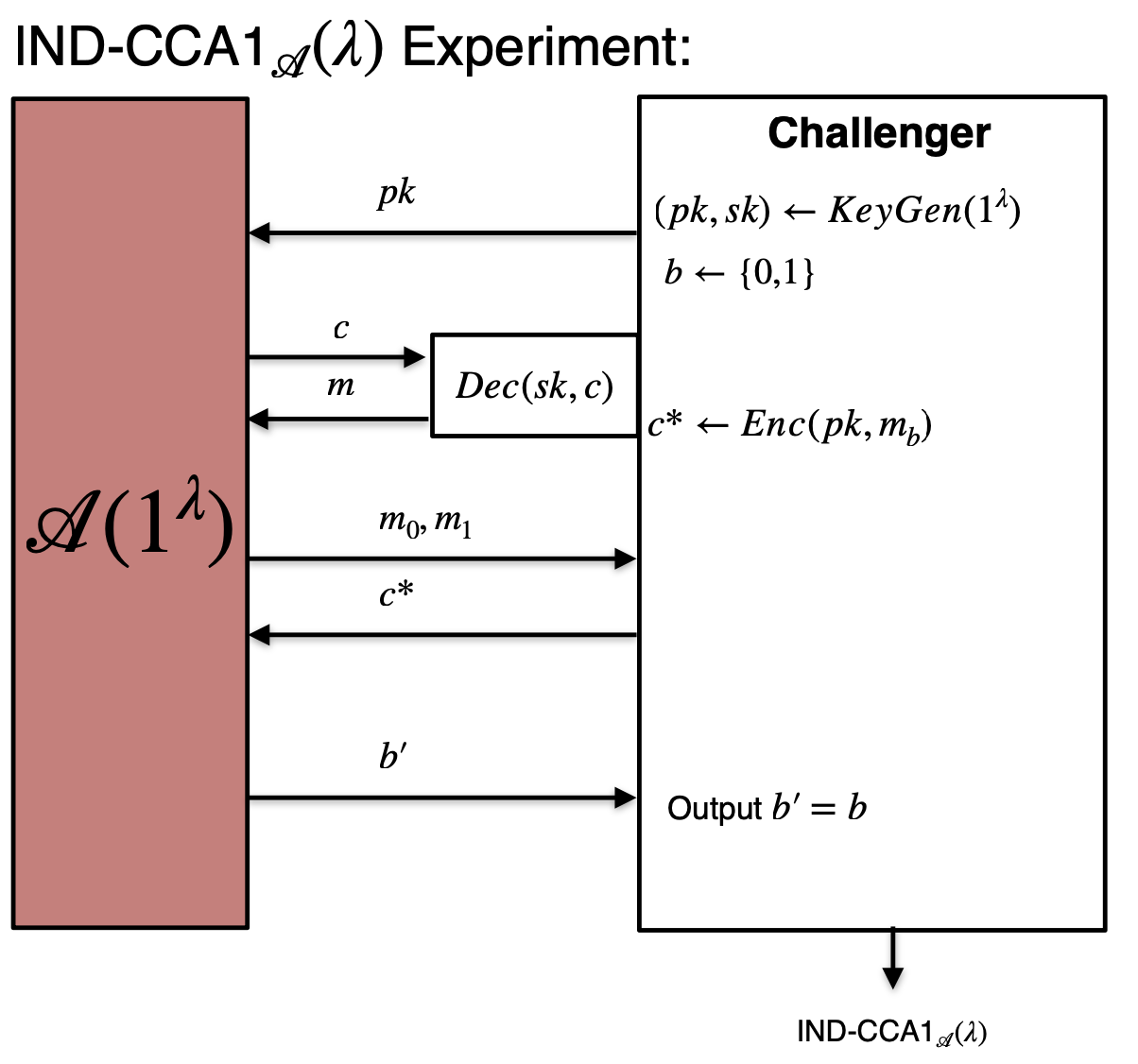
这就是常见的CCA安全的定义。这其实是CCA 2的安全性定义，注意第4步，我们加*号，这里允许攻击者可以继续选择密文得到新的解密结果，这也就是自适应的含义，攻击者在攻击过程中可以自由地查询解密函数，甚至在看到攻击目标密文后仍然能够继续查询解密过程。但攻击者不能直接查询目标密文本身。然而CCA 1实验中，一旦攻击者得到要攻击的密文，就不能再继续查询解密结果。

通过这些定义，我们会发现ElGamal加密方案不是CCA安全的，CCA1都达不到，只能保证CPA安全。具体而言，ElGamal 加密像是一个同态加密方案，这意味着密文的组合运算可以映射到明文上的某种操作。通过修改ElGamal得到的Hashed ElGamal系统就可以实现CCA安全，就是通过哈希来破坏数学对应关系。